 |
|||||||
|
|

|
Displacement flows
Synopsis : Displacement and removal flows are widespread in natural phenomena and industrial applications, including oil and gas industries, food processing, manufacturing, personal care, and biomedical applications. These flows aim to displace or remove an in-situ fluid by introducing another fluid with different physical properties. Understanding these flows can be challenging due to the many parameters affecting interface motion, including density and viscosity ratios, injection rates, geometry, miscibility, and non-Newtonian rheology. This body of work focuses on exploring these parameters to better understand displacement flow and develop more effective interface controlling methods. |
Viscoplastic fluid displacement flows in horizontal channels: Numerical simulations
Buoyant miscible displacement flows of Newtonian fluids in vertical pipe
Displacement and exchange flows in axially rotating pipes
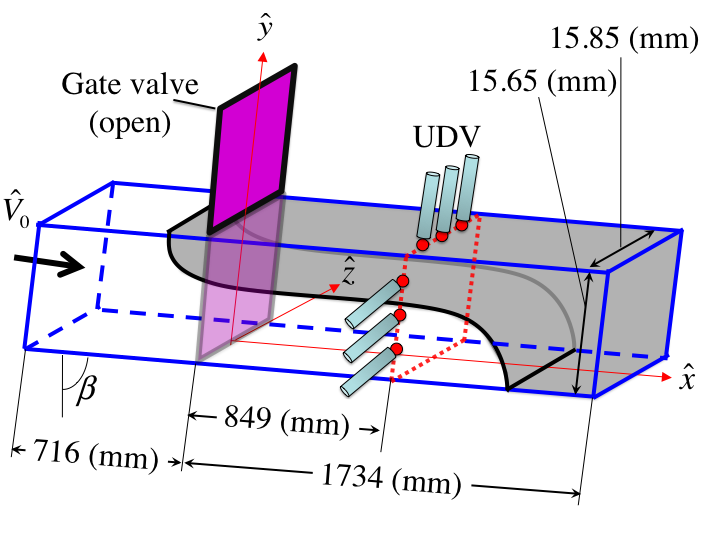
Displacement flows in a non-uniform channel
Displacement and exchange flows in axially rotating pipes
|
Viscoplastic fluid injection flows
Synopsis: Viscoplastic fluid injection into another is a common process in industries such as oil and gas wells, injection molding and 3D printing. The analysis of these processes involves quantifying the interface between the fluids, with the yielding behavior of the viscoplastic fluid being a key factor. However, the analysis is complicated due to the presence of various flow parameters, such as density and viscosity ratios, flow geometry characteristics, and yield stress, resulting in different flow patterns. |
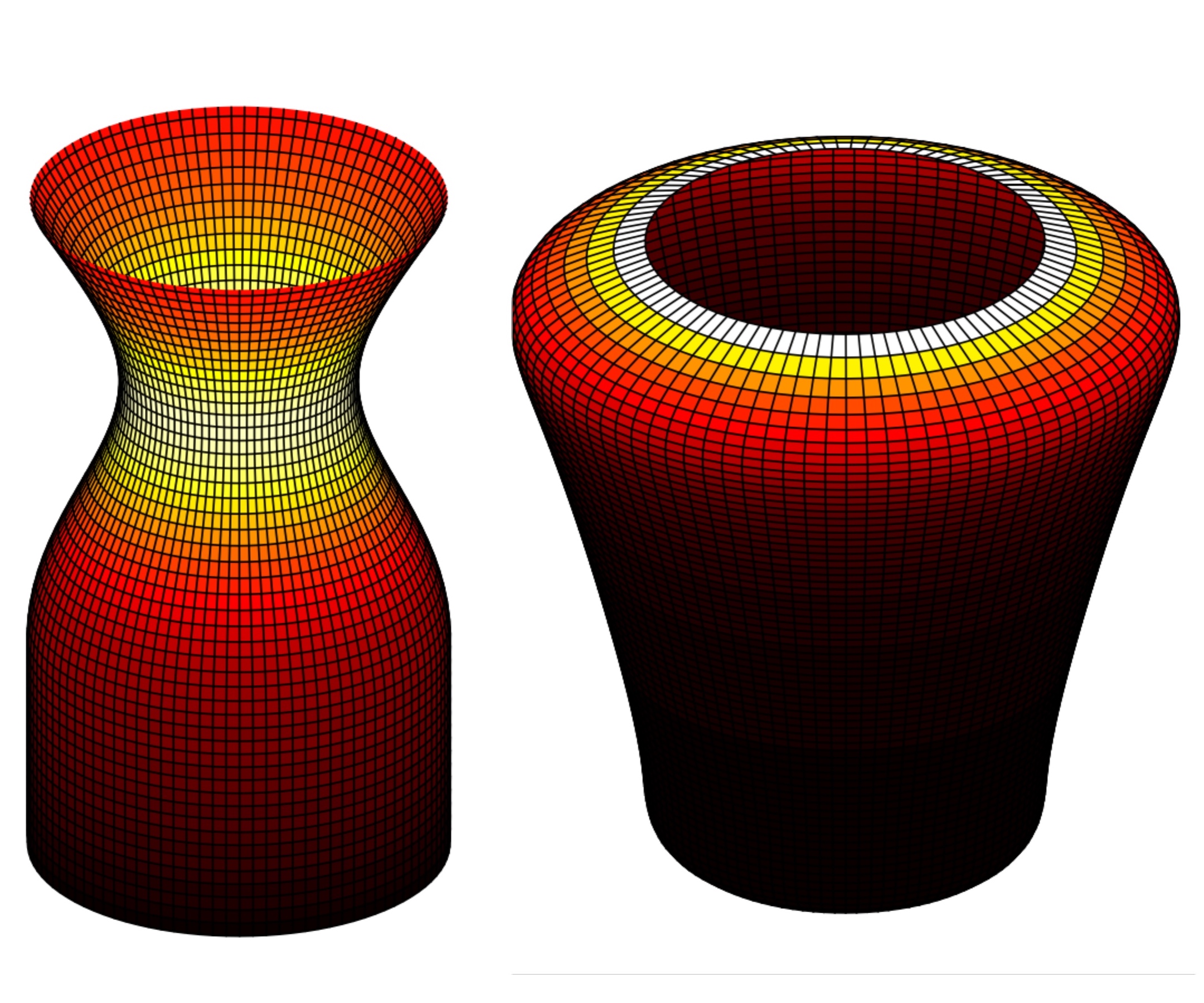
From breakup to coiling and buckling regimes in buoyant viscoplastic injections
Dynamics of the buoyant injection of a viscoplastic fluid in a confined geometry
|
Jet flows
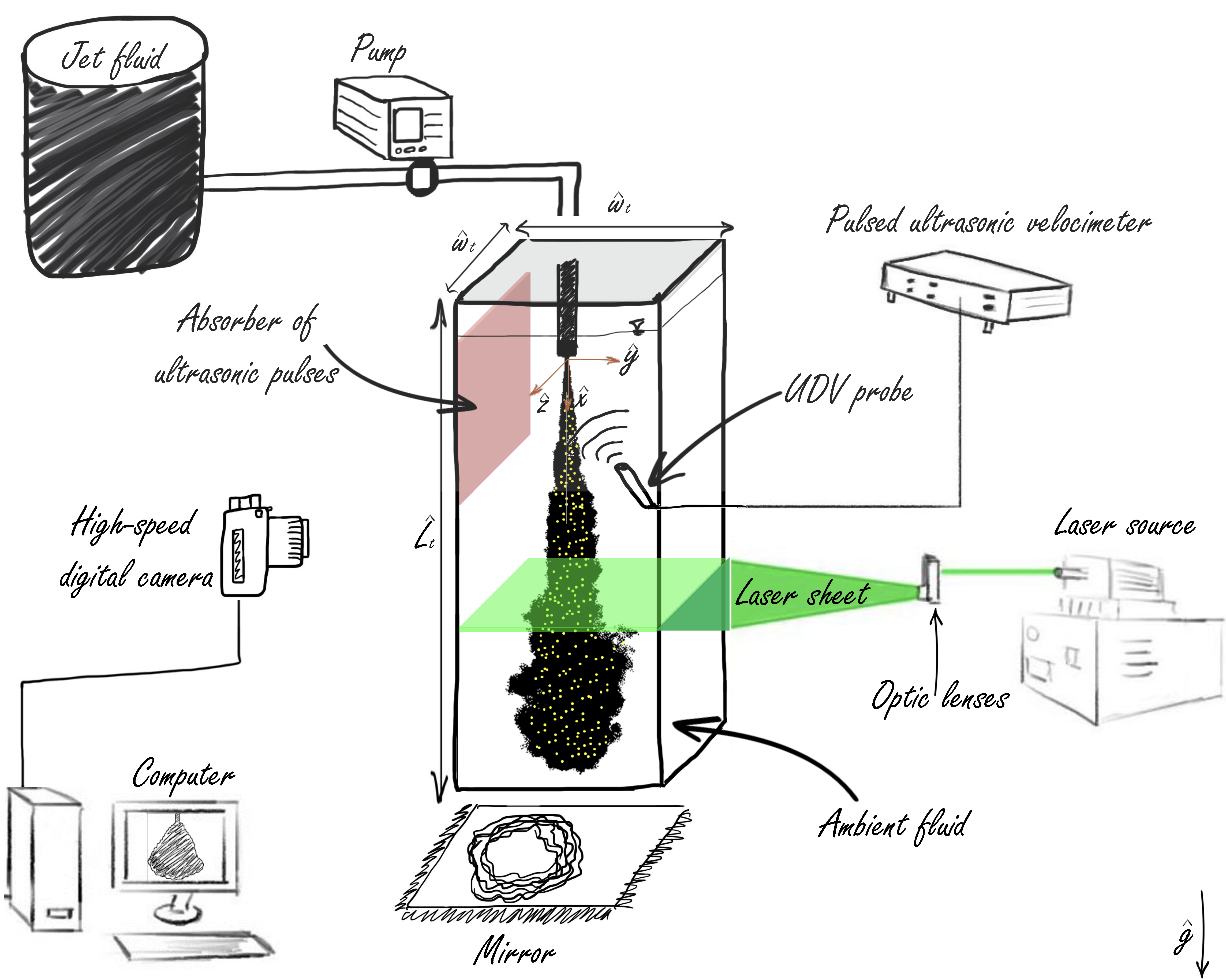
Synopsis: Jet flows are common in environmental, medical and industrial applications, but their behavior is not yet fully understood. In this work, we study the injection of fluid into another fluid with different densities, for example for cleaning processes, and explore the jet flow behavior and its effect on cleaning efficiency. |
Fluid injection into a viscoplastic fluid
|
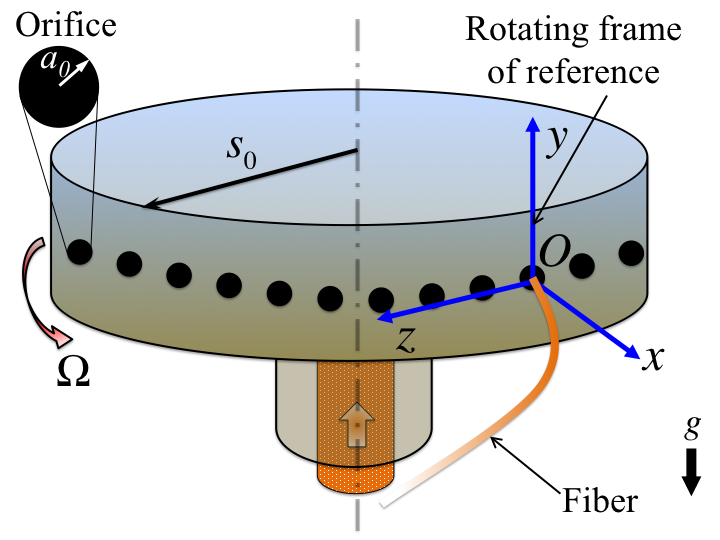
Nanofibre formation via centrifugal spinning
Synopsis: We model and run experiments for a new process called the centrifugal spinning process which has greatly improved the production of nanofibers. However, controlling the fiber diameter and morphology is a challenge in this process due to the large number of flow parameters. Our group has made groundbreaking progress by developing advanced models, validated by experiments, that predict the nanofiber formation dynamics with high precision, taking into account various factors such as viscous, inertial, rotational, surface tension, gravitational, mass diffusion, aerodynamic and non-Newtonian rheological effects. Collaborators: Professor R.G. Larson at University of Michigan and Dr. W. Arne at Fraunhofer Institute for Industrial Mathematics. |
Nanofiber formation through centrifugal spinning
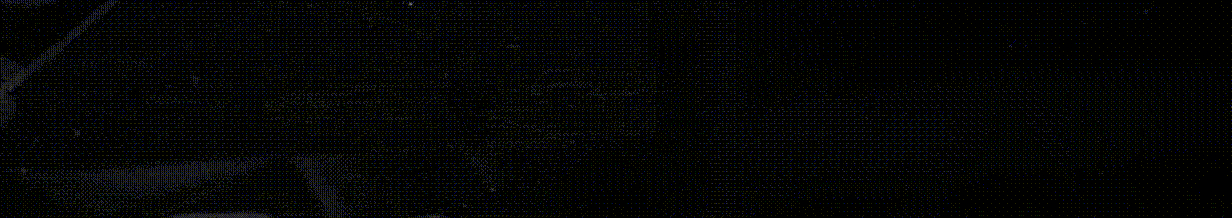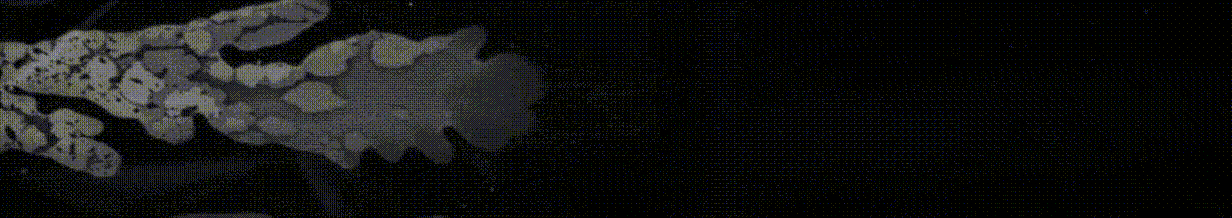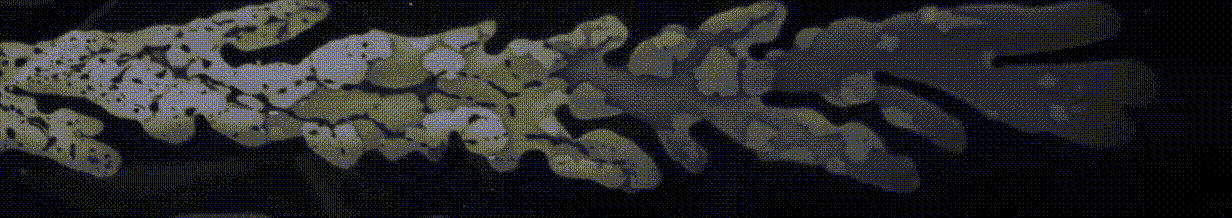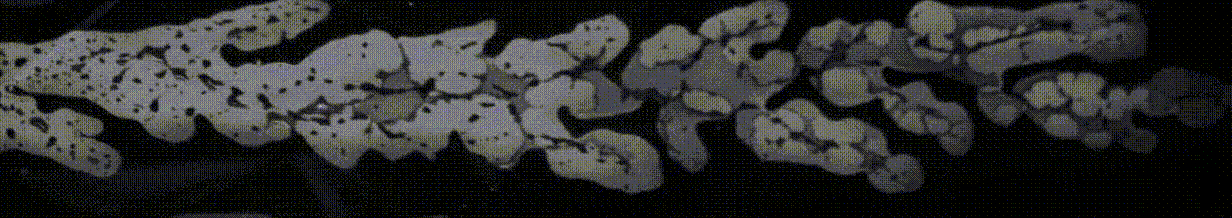
|
Elasto-visco-plastic fingering
Synopsis: We explore the patterns formed by interfacial instabilities, based on the Saffman-Taylor instability or viscous fingering, which occurs when air displaces a viscous liquid. We experimentally study this instability in elasto-visco-plastic fluids, which exhibit viscous, plastic and elastic behaviors, and observe various flow regimes. Our findings shed light on the complex behavior of complex fluids in viscous fingering. |
Viscous fingering regimes in elasto-visco-plastic fluids
|
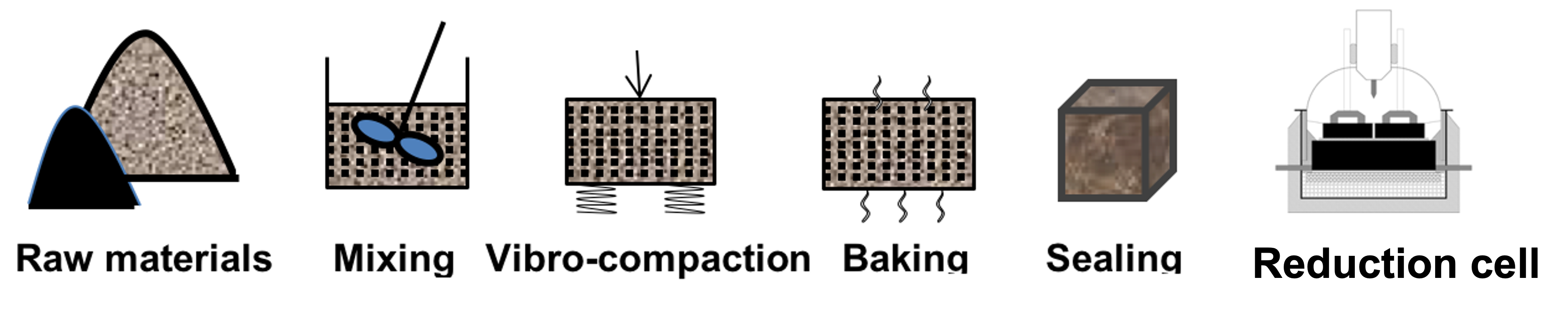
Aluminum production process
Synopsis: While Canada has a thriving aluminum industry, aluminum production processes are concerned with serious environment and energy issues. To tackle these problems, we have teamed up with experts in metallurgy, materials, chemistry, and fluid mechanics, and computer models, simulations, and experiments to find solutions. Collaborators: Professor H. Alamdari and Professor Gosselin at Laval. |
|
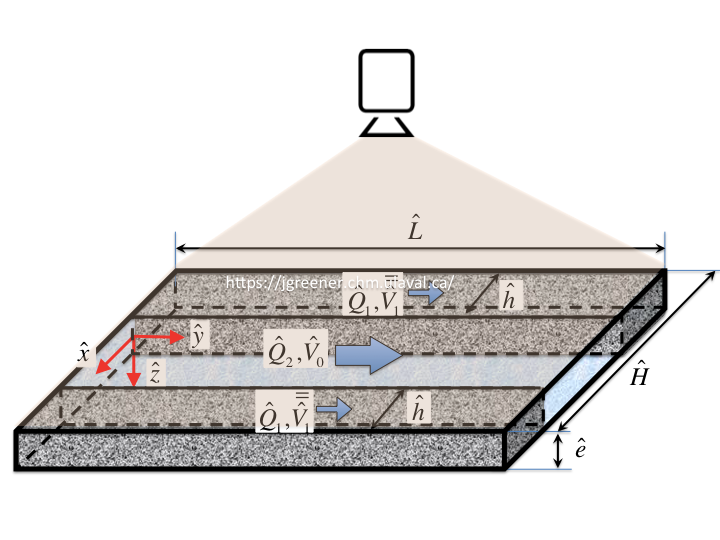
Rheological characterisations of biofilm via modelling and experiments
Synopsis: Bacterial biofilms are slimy structures made of bacteria, polymers, DNAs, and proteins that can cause problems, but also have useful applications. We work with experts in chemistry, biology, and fluid mechanics to create mathematical models that help us understand and predict biofilm rheological properties. By using non-intrusive optical measurements and flow models, we can accurately characterize biofilm rheology and other properties under different conditions like temperature, ionic strength, and shear stress. This research can be used to study biofilm mechanical properties, which can have important applications in environmental and biological studies, biofouling control, and biocatalyst development. Collaborators: Professor J. Greener at Laval. |




|
Multiphase flows in moving geometry
Synopsis: We work with marine, engineering and chemistry experts to study how multiphase flows in floating scrubbers and reactors on ships. These machines clean the air and water on ships, but multiphase flow physics may be affected by ship motion, which we study by simulations and experiments, for example via a hexapod robot capable of imposing six different degrees of motion freedom. Collaborators: Professor F. Larachi at Laval. |







